README.md

题目描述: 地图分析

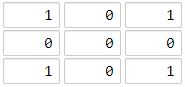
你现在手里有一份大小为 N x N 的『地图』（网格） grid，上面的每个『区域』（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，你知道距离陆地区域最远的海洋区域是是哪一个吗？请返回该海洋区域到离它最近的陆地区域的距离。

我们这里说的距离是『曼哈顿距离』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。

示例 :

输入：[[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。

解题思路:

理解题意：其实就是找到一个海洋区域，这个海洋区域到与它最近的陆地区域的距离是最大的。那么就是按照层序遍历，最后一个遍历到的海洋就是所求。

二维表格上的问题，常用的算法是深度优先遍历、广度优先遍历和并查集，由于这里计算的结果和距离相关，显然使用广度优先遍历；

一般而言，「广度优先遍历」求的是最短路径，但仔细一想，发现其实广度优先遍历也是适用的：

• 求最短路径的时候，只要找到目标值，返回即可；
• 求最长路径的时候，所有目标值都看完以后，才返回。

广度优先遍历（BFS）逐层向外扩散的精准数学解释，每扩散一次，曼哈顿距离就加 1。

时间复杂度：

O(n**n) 这里 n 是方格的边长。二维表格里所有的元素都会被看一遍；

空间复杂度

O(n**n) 最坏情况下，方格里全部是陆地（1）的时候，元素全部会进队列。

代码

bfs

class Solution {
public:
    int maxDistance(vector<vector<int>>& grid) {
        if (grid.empty()) return 0;
        int n = grid.size();
        queue<pair<int,int>> q;
        vector<int> dx {1,-1,0,0};
        vector<int> dy {0,0,1,-1};
        int res = 0;
        for (int i=0;i<n;i++)
        {
            for (int j=0;j<n;j++)
            {
                if (grid[i][j]==1)
                {
                    q.push(make_pair(i,j));
                }
            }
        }
        int m = q.size();
        if (m ==0||m==n*n) return -1;
        while(!q.empty())
        {
            int size = q.size();
            for (int i=0;i<size;i++)
            {
                pair<int,int> d = q.front();
                q.pop();
                for (int k=0;k<4;k++)
                {
                    int x = d.first + dx[k];
                    int y = d.second + dy[k]
                    // 只关心有效范围内的海洋（0）;
                    if (x>=0 && x<n && y>=0 && y<n && grid[x][y]==0)
                    {
                        grid[x][y] = 1;
                        q.push(make_pair(x,y));
                    }
                }
            }
            if (!q.empty())res++;
        }
        return res;
    }
};