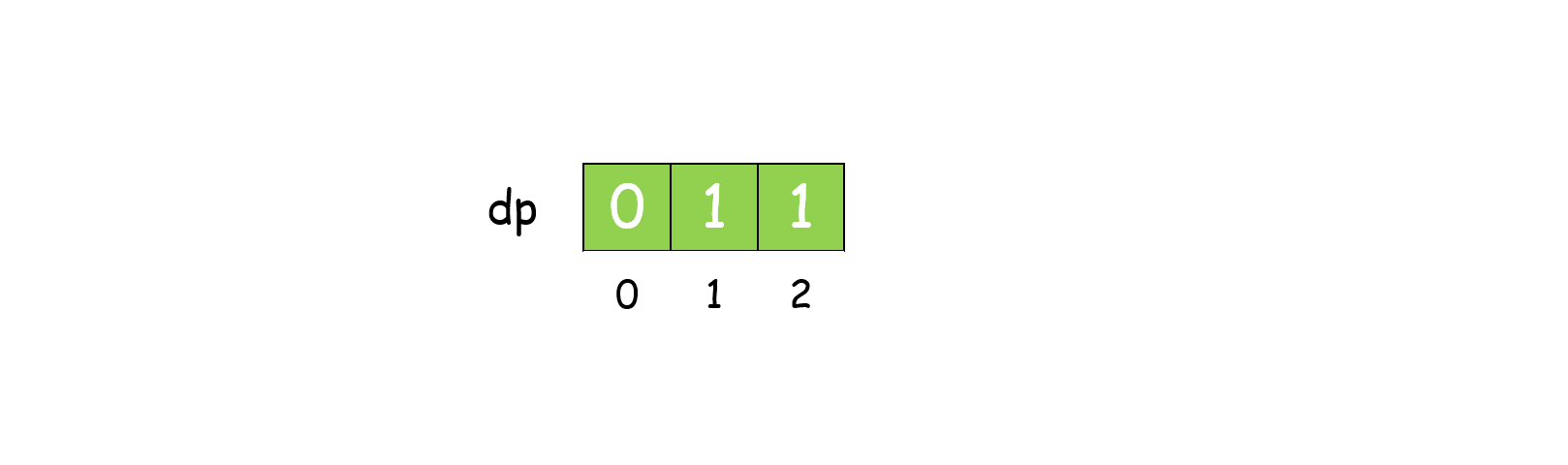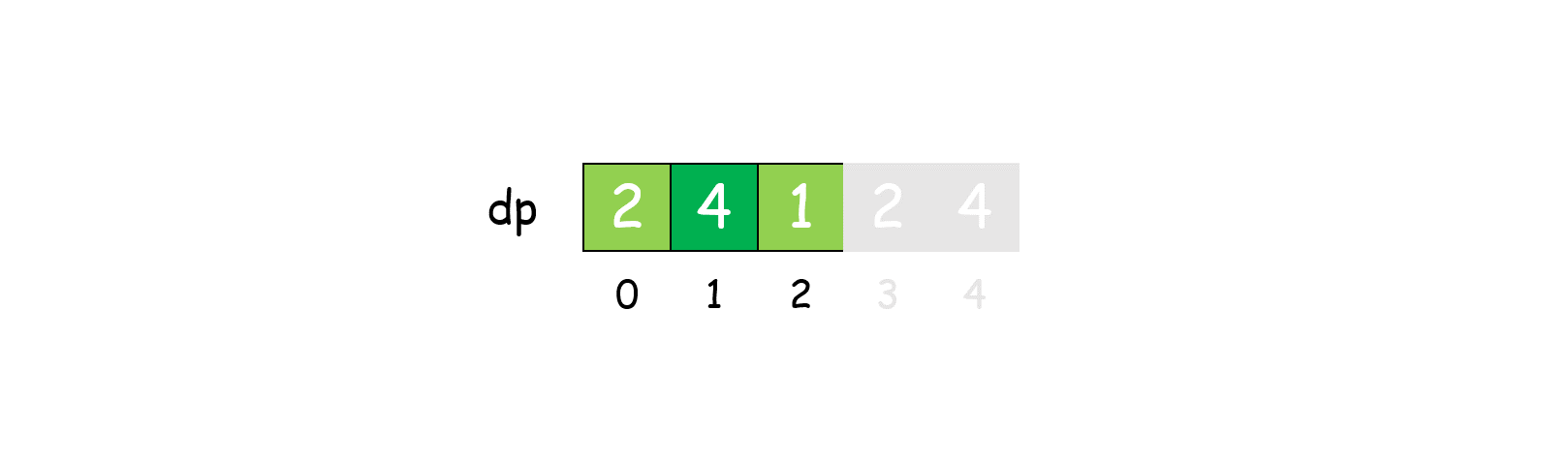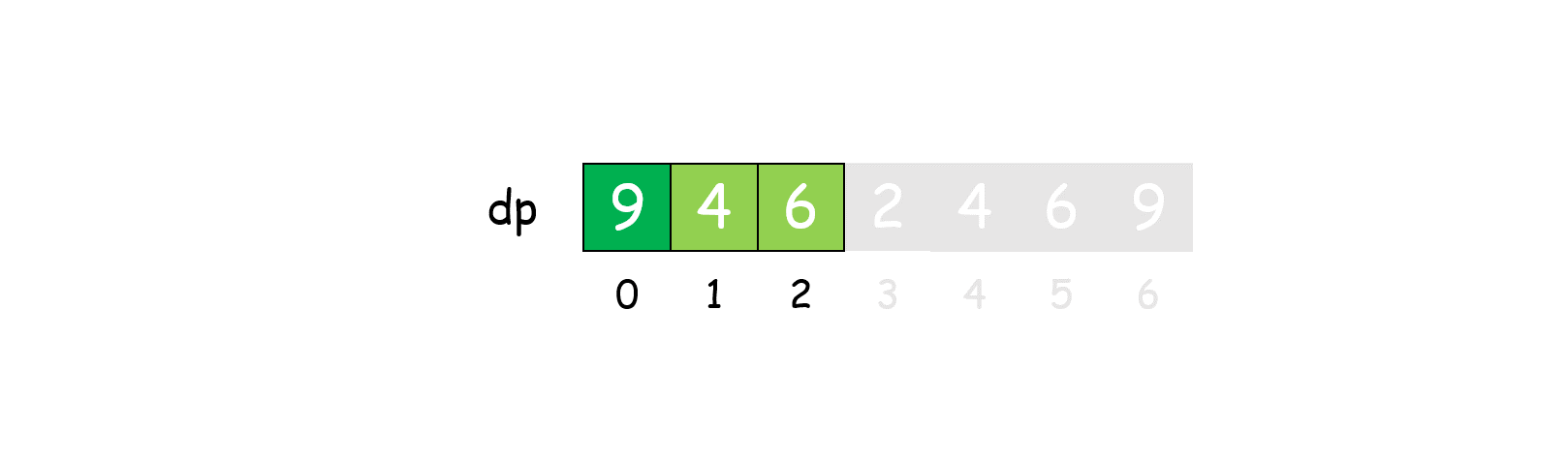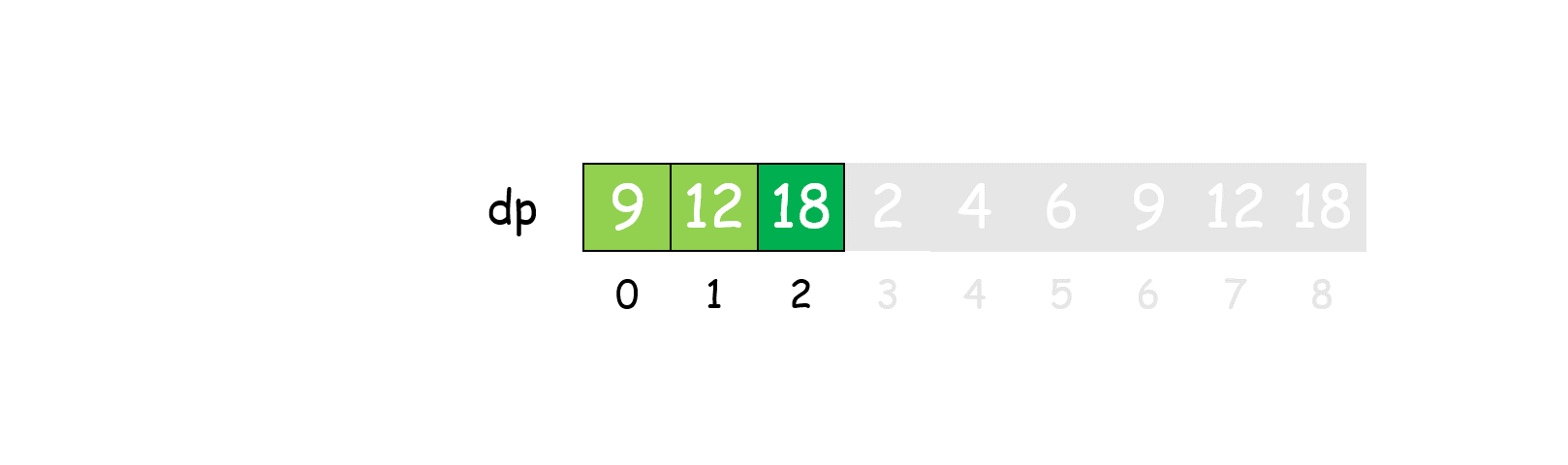README.md

题目: 剪绳子

题目描述：

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m] 。请问 k[0]*k[1]*...*k[m] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例2：

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

解题思路:

1. 动态规划，从已知值 F(2)逐步迭代到目标值 F(n)，它是一种自底向上的方法。

建立一维动态数组 dp：

• 定义状态：定义 dp[i] 表示长度i的绳子能得到的最大乘积
• 边界条件：dp[1] = dp[2] = 1，表示长度为 2 的绳子最大乘积为 1；
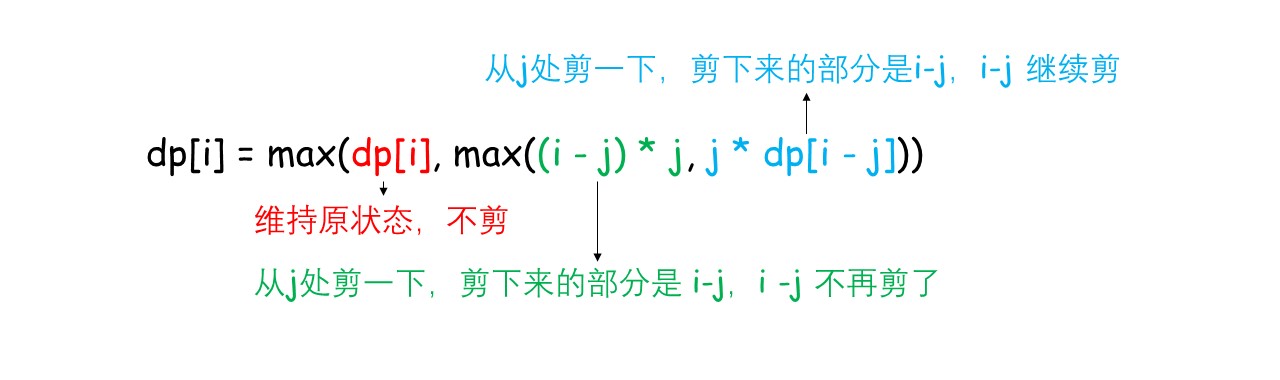
• 状态转移方程：dp[i] = max(dp[i], max((i - j) * j, j * dp[i - j]))，可以这样理解：

2. 动态规划优化，任何大于 3的数都可以拆分为数字 1，2，3的和，且它们对 3的余数总是 0，1，2，因此我们可以仅用 dp[0]，dp[1]，dp[2] 表示所有大于 3 的值，这样空间复杂度可降到 O(1)。

3. 贪心算法

数学推导

时间复杂度：

1： O(n^2)

2: O(n);

3: O(1);

空间复杂度

1: O(n)

2: O(1)

3: O(1)

代码

C++

Python

C++:

动态规划（自底向上）

class Solution {
public:
    int cuttingRope(int n) {
        vector<int> dp (n+1,0); 
        dp[1] = 1;
        dp[2] = 1;
        for (int i=3;i<=n;i++)
        {
            for(int j=1;j<=i-1;j++)
            {
                dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]));
            }
        }
        return dp[n];
    }
};

动态规划（优化）

class Solution {
public:
    int cuttingRope(int n) {
        vector<int> dp(3,1);
        dp[0] = 0;
        for (int i=3;i<=n;i++)
        {
            dp[i % 3] = max((max(dp[(i-1)%3],i-1)),
            max((2*max(dp[(i-2)%3], i-2)), (3*max(dp[(i-3)%3]
            i-3))));
        }
        return dp[n%3];
    }
};

贪心算法

class Solution {
public:
    int cuttingRope(int n) {
        if (n<=3)
            return n-1;
        int a = n/3;
        int b = n%3;
        if (b==0)
            return pow(3,a);
        if (b==1)
            return pow(3,a-1)*4;
        return pow(3,a)*2;
    }
};

Python:

动态规划

class Solution:
    def cuttingRope(self, n: int) -> int:
        dp = [0 for _ in range(n+1)]
        dp[2] = 1
        for i in range(3,n+1):
            for j in range(1,  i-1):
                dp[i] = max(dp[i], j*(i-j), j*dp[i-j])
        return dp[n]

动态规划（优化版）

class Solution:
    def cuttingRope(self, n: int) -> int:
        dp = [0, 1, 1]

        for i in range(3, n + 1):
            dp[i % 3] = max(max(dp[(i - 1) % 3], i - 1),
                    2 * max(dp[(i - 2) % 3], i - 2),
                    3 * max(dp[(i - 3) % 3], i - 3))
        return dp[n % 3]

贪心算法

Python 中常见有三种幂计算函数： ** 和 pow() 的时间复杂度均为 O(loga)；而 math.pow() 始终调用 C 库的 pow() 函数，其执行浮点取幂，时间复杂度为 O(1) 。

class Solution:
    def cuttingRope(self, n: int) -> int:
        if n <= 3: return n - 1
        a, b = n // 3, n % 3
        if b == 0: return int(math.pow(3, a))
        if b == 1: return int(math.pow(3, a - 1) * 4)
        return int(math.pow(3, a) * 2)